반응형
https://www.udacity.com/course/artificial-intelligence-for-robotics--cs373
Artificial Intelligence for Robotics | Udacity Free Courses
Take Udacity's Artificial Intelligence of Robotics course and learn how to program all the major systems of a robotic car. Learn online with Udacity.
www.udacity.com
Lesson 1 : Localization Overview
1. Introduction
2. Nanodegree Program
3. Localization
- GPS는 2~10m 오차를 가짐
- 자율주행을 위해서는 2~10 cm의 오차가 필요
4. Total Probability

5. Uniform Probabilty Quiz

6. Uniform Distribution
# Modify the empty list, p, so that it becomes a UNIFORM probability
# distribution over five grid cells, as expressed in a list of
# five probabilities.
p = [0.2, 0.2, 0.2, 0.2, 0.2]
print p
# [0.2, 0.2, 0.2, 0.2, 0.2]7. Generalized Uniform Distribution
# Modify your code to create probability vectors, p, of arbitrary
# size, n. Use n=5 to verify that your new solution matches
# the previous one.
p=[]
n=5
for _ in range(n):
p.append(1./n)
print p
# [0.2, 0.2, 0.2, 0.2, 0.2]8. Probability After Sense

9. Compute Sum

10. Normalize Distribution

11. pHit and pMiss
#Write code that outputs p after multiplying each entry
#by pHit or pMiss at the appropriate places. Remember that
#the red cells 1 and 2 are hits and the other green cells
#are misses.
p=[0.2,0.2,0.2,0.2,0.2]
pHit = 0.6
pMiss = 0.2
#Enter code here
for i in range(len(p)):
if i==1 or i==2:
p[i] = p[i]*pHit
else:
p[i] = p[i]*pMiss
print p
# [0.04000000000000001, 0.12, 0.12, 0.04000000000000001, 0.04000000000000001]12. Sum of Probabilities
#Modify the program to find and print the sum of all
#the entries in the list p.
p=[0.2, 0.2, 0.2, 0.2, 0.2]
pHit = 0.6
pMiss = 0.2
p[0]=p[0]*pMiss
p[1]=p[1]*pHit
p[2]=p[2]*pHit
p[3]=p[3]*pMiss
p[4]=p[4]*pMiss
# Enter your code below
print sum(p)
# 0.3613. Sense Function
#Modify the code below so that the function sense, which
#takes p and Z as inputs, will output the NON-normalized
#probability distribution, q, after multiplying the entries
#in p by pHit or pMiss according to the color in the
#corresponding cell in world.
p=[0.2, 0.2, 0.2, 0.2, 0.2]
world=['green', 'red', 'red', 'green', 'green']
Z = 'red'
pHit = 0.6
pMiss = 0.2
def sense(p, Z):
#ADD YOUR CODE HERE
q = []
for i, z in enumerate(world):
if z == Z:
q.append(p[i]*pHit)
else:
q.append(p[i]*pMiss)
return q
print sense(p,Z)
# [0.04000000000000001, 0.12, 0.12, 0.04000000000000001, 0.04000000000000001]14. Normalized Sense Function
#Modify your code so that it normalizes the output for
#the function sense. This means that the entries in q
#should sum to one.
p=[0.2, 0.2, 0.2, 0.2, 0.2]
world=['green', 'red', 'red', 'green', 'green']
Z = 'red'
pHit = 0.6
pMiss = 0.2
def sense(p, Z):
q=[]
for i in range(len(p)):
hit = (Z == world[i])
q.append(p[i] * (hit * pHit + (1-hit) * pMiss))
# Nomalize
s = sum(q)
for i in range(len(q)):
q[i] = q[i]/s
return q
print sense(p,Z)
# [0.1111111111111111, 0.3333333333333332, 0.3333333333333332, 0.1111111111111111, 0.1111111111111111]15. Test Sense Function
#Try using your code with a measurement of 'green' and
#make sure the resulting probability distribution is correct.
p=[0.2, 0.2, 0.2, 0.2, 0.2]
world=['green', 'red', 'red', 'green', 'green']
Z = 'green'
pHit = 0.6
pMiss = 0.2
def sense(p, Z):
q=[]
for i in range(len(p)):
hit = (Z == world[i])
q.append(p[i] * (hit * pHit + (1-hit) * pMiss))
s = sum(q)
for i in range(len(p)):
q[i]=q[i]/s
return q
print sense(p, Z)
# [0.2727272727272727, 0.09090909090909093, 0.09090909090909093, 0.2727272727272727, 0.2727272727272727]16. Multiple Measurements
#Modify the code so that it updates the probability twice
#and gives the posterior distribution after both
#measurements are incorporated. Make sure that your code
#allows for any sequence of measurement of any length.
p=[0.2, 0.2, 0.2, 0.2, 0.2]
world=['green', 'red', 'red', 'green', 'green']
measurements = ['red', 'green']
pHit = 0.6
pMiss = 0.2
def sense(p, Z):
q=[]
for i in range(len(p)):
hit = (Z == world[i])
q.append(p[i] * (hit * pHit + (1-hit) * pMiss))
s = sum(q)
for i in range(len(q)):
q[i] = q[i] / s
return q
#ADD YOUR CODE HERE
for m in measurements:
p = sense(p, m)
print p
# [0.20000000000000004, 0.19999999999999996, 0.19999999999999996, 0.20000000000000004, 0.20000000000000004]17. Lesson Breakpoint
18. Exact Motion
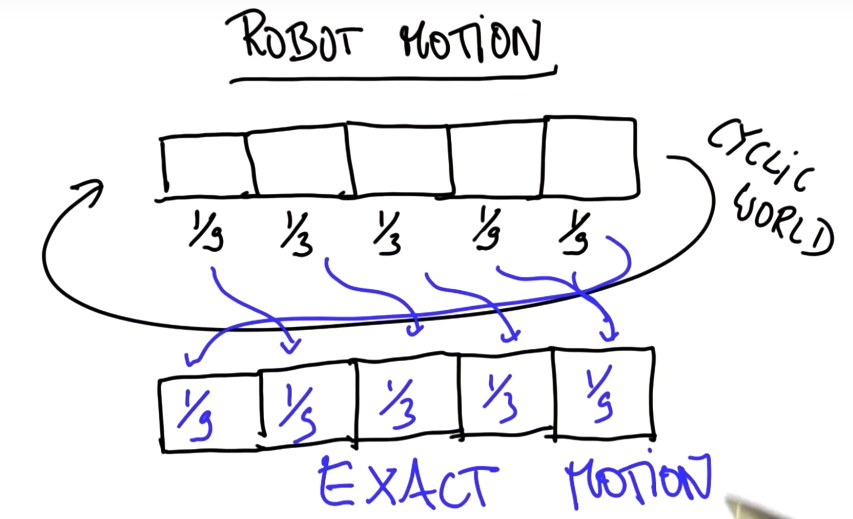
19. Move Function
#Program a function that returns a new distribution
#q, shifted to the right by U units. If U=0, q should
#be the same as p.
p=[0, 1, 0, 0, 0]
world=['green', 'red', 'red', 'green', 'green']
measurements = ['red', 'green']
pHit = 0.6
pMiss = 0.2
def sense(p, Z):
q=[]
for i in range(len(p)):
hit = (Z == world[i])
q.append(p[i] * (hit * pHit + (1-hit) * pMiss))
s = sum(q)
for i in range(len(q)):
q[i] = q[i] / s
return q
def move(p, U):
#ADD CODE HERE
q = p[-U:] + p[:-U]
return q
print move(p, 1)
# [0, 0, 1, 0, 0]20. Inexact Motion1
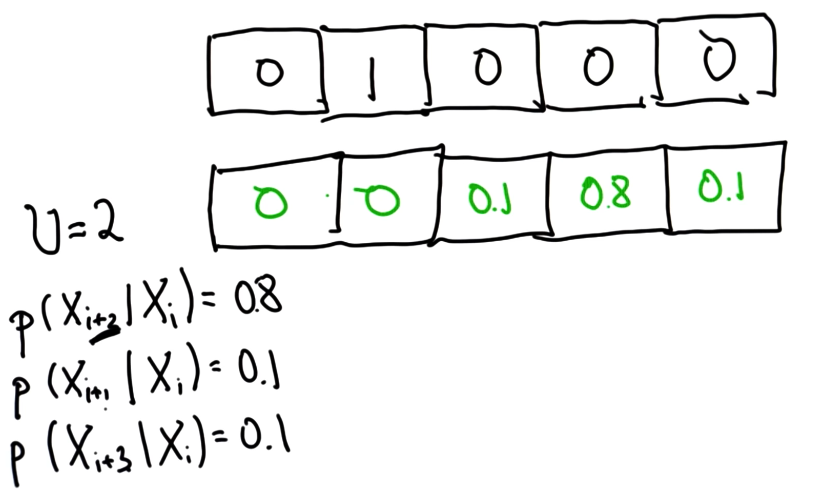
21. Inexact Motion2
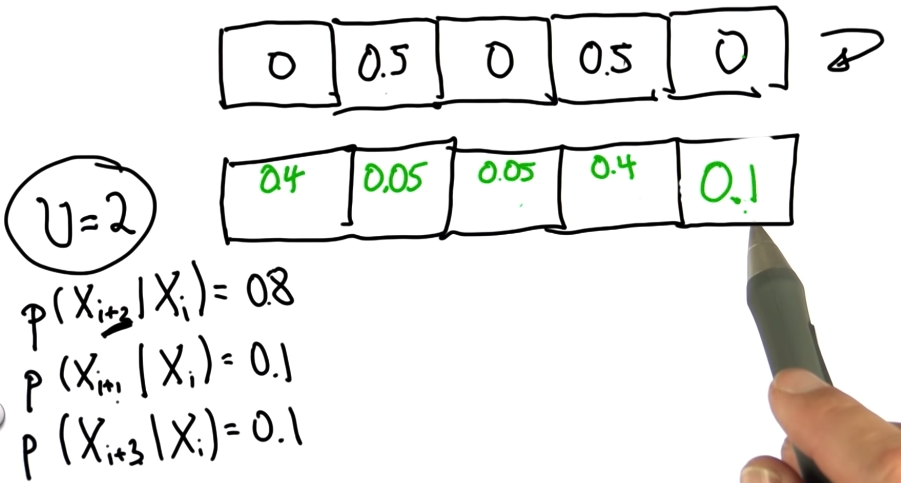
22. Inexact Motion3
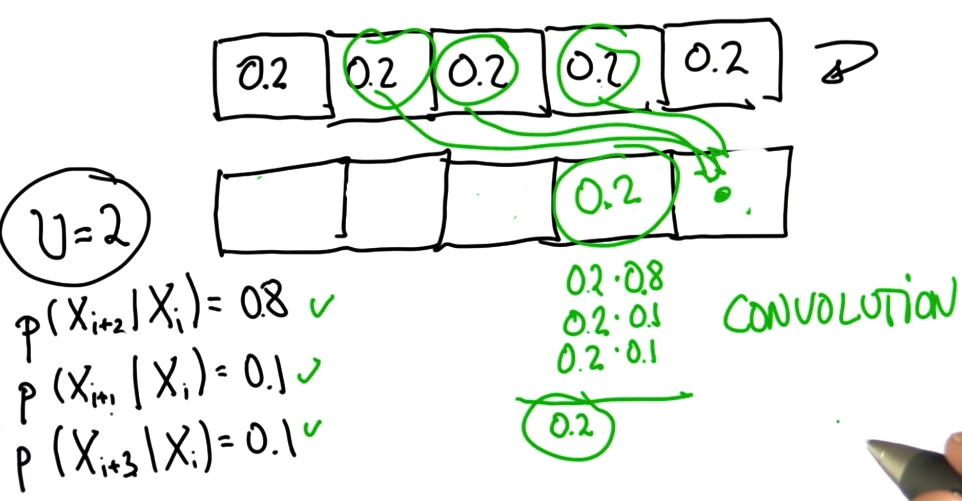
23. Inexact Move Function
#Modify the move function to accommodate the added
#probabilities of overshooting or undershooting
#the intended destination.
p=[0, 1, 0, 0, 0]
world=['green', 'red', 'red', 'green', 'green']
measurements = ['red', 'green']
pHit = 0.6
pMiss = 0.2
pExact = 0.8
pOvershoot = 0.1
pUndershoot = 0.1
def sense(p, Z):
q=[]
for i in range(len(p)):
hit = (Z == world[i])
q.append(p[i] * (hit * pHit + (1-hit) * pMiss))
s = sum(q)
for i in range(len(q)):
q[i] = q[i] / s
return q
def move(p, U):
q = []
for i in range(len(p)):
s = pOvershoot * p[(i-U+1)%len(p)]
s = s + pExact * p[(i-U)%len(p)]
s = s + pUndershoot * p[(i-U-1)%len(p)]
q.append(s)
return q
print move(p, 1)
# [0.0, 0.1, 0.8, 0.1, 0.0]24. Limit Distribution Quiz

25. Move Twice
# Write code that makes the robot move twice and then prints
# out the resulting distribution, starting with the initial
# distribution p = [0, 1, 0, 0, 0]
p=[0, 1, 0, 0, 0]
world=['green', 'red', 'red', 'green', 'green']
measurements = ['red', 'green']
pHit = 0.6
pMiss = 0.2
pExact = 0.8
pOvershoot = 0.1
pUndershoot = 0.1
def sense(p, Z):
q=[]
for i in range(len(p)):
hit = (Z == world[i])
q.append(p[i] * (hit * pHit + (1-hit) * pMiss))
s = sum(q)
for i in range(len(q)):
q[i] = q[i] / s
return q
def move(p, U):
q = []
for i in range(len(p)):
s = pExact * p[(i-U) % len(p)]
s = s + pOvershoot * p[(i-U-1) % len(p)]
s = s + pUndershoot * p[(i-U+1) % len(p)]
q.append(s)
return q
# ADD CODE HERE
p = move(p, 1)
p = move(p, 1)
# Make sure to print out p!
print p
# [0.010000000000000002, 0.010000000000000002, 0.16000000000000003, 0.6600000000000001, 0.16000000000000003]26. Move 1000
#write code that moves 1000 times and then prints the
#resulting probability distribution.
p=[0, 1, 0, 0, 0]
world=['green', 'red', 'red', 'green', 'green']
measurements = ['red', 'green']
pHit = 0.6
pMiss = 0.2
pExact = 0.8
pOvershoot = 0.1
pUndershoot = 0.1
def sense(p, Z):
q=[]
for i in range(len(p)):
hit = (Z == world[i])
q.append(p[i] * (hit * pHit + (1-hit) * pMiss))
s = sum(q)
for i in range(len(q)):
q[i] = q[i] / s
return q
def move(p, U):
q = []
for i in range(len(p)):
s = pExact * p[(i-U) % len(p)]
s = s + pOvershoot * p[(i-U-1) % len(p)]
s = s + pUndershoot * p[(i-U+1) % len(p)]
q.append(s)
return q
# ADD CODE HERE
for _ in range(1000):
p = move(p, 1)
print p
# [0.20000000000000365, 0.20000000000000373, 0.20000000000000365, 0.2000000000000035, 0.2000000000000035]27. Sense and Move
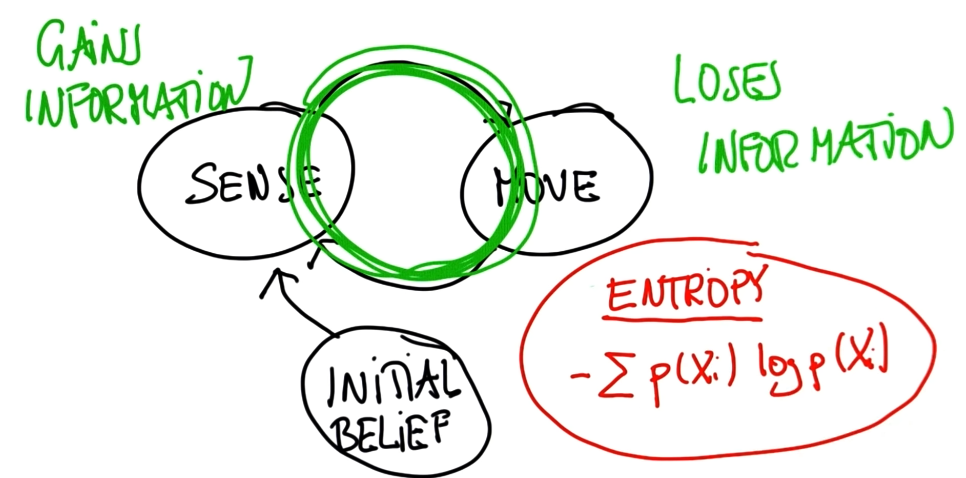
#Given the list motions=[1,1] which means the robot
#moves right and then right again, compute the posterior
#distribution if the robot first senses red, then moves
#right one, then senses green, then moves right again,
#starting with a uniform prior distribution.
p=[0.2, 0.2, 0.2, 0.2, 0.2]
world=['green', 'red', 'red', 'green', 'green']
measurements = ['red', 'green']
motions = [1,1]
pHit = 0.6
pMiss = 0.2
pExact = 0.8
pOvershoot = 0.1
pUndershoot = 0.1
def sense(p, Z):
q=[]
for i in range(len(p)):
hit = (Z == world[i])
q.append(p[i] * (hit * pHit + (1-hit) * pMiss))
s = sum(q)
for i in range(len(q)):
q[i] = q[i] / s
return q
def move(p, U):
q = []
for i in range(len(p)):
s = pExact * p[(i-U) % len(p)]
s = s + pOvershoot * p[(i-U-1) % len(p)]
s = s + pUndershoot * p[(i-U+1) % len(p)]
q.append(s)
return q
# ADD CODE HERE
p = sense(p, 'red')
p = move(p, 1)
p = sense(p, 'green')
p = move(p, 1)
print p
# [0.21157894736842103, 0.1515789473684211, 0.08105263157894739, 0.16842105263157897, 0.3873684210526316]28. Sense and Move2
#Modify the previous code so that the robot senses red twice.
p=[0.2, 0.2, 0.2, 0.2, 0.2]
world=['green', 'red', 'red', 'green', 'green']
measurements = ['red', 'red']
motions = [1,1]
pHit = 0.6
pMiss = 0.2
pExact = 0.8
pOvershoot = 0.1
pUndershoot = 0.1
def sense(p, Z):
q=[]
for i in range(len(p)):
hit = (Z == world[i])
q.append(p[i] * (hit * pHit + (1-hit) * pMiss))
s = sum(q)
for i in range(len(q)):
q[i] = q[i] / s
return q
def move(p, U):
q = []
for i in range(len(p)):
s = pExact * p[(i-U) % len(p)]
s = s + pOvershoot * p[(i-U-1) % len(p)]
s = s + pUndershoot * p[(i-U+1) % len(p)]
q.append(s)
return q
for k in range(len(measurements)):
p = sense(p, measurements[k])
p = move(p, motions[k])
print p
# [0.07882352941176471, 0.07529411764705884, 0.22470588235294123, 0.4329411764705882, 0.18823529411764706]29. Localization Summary
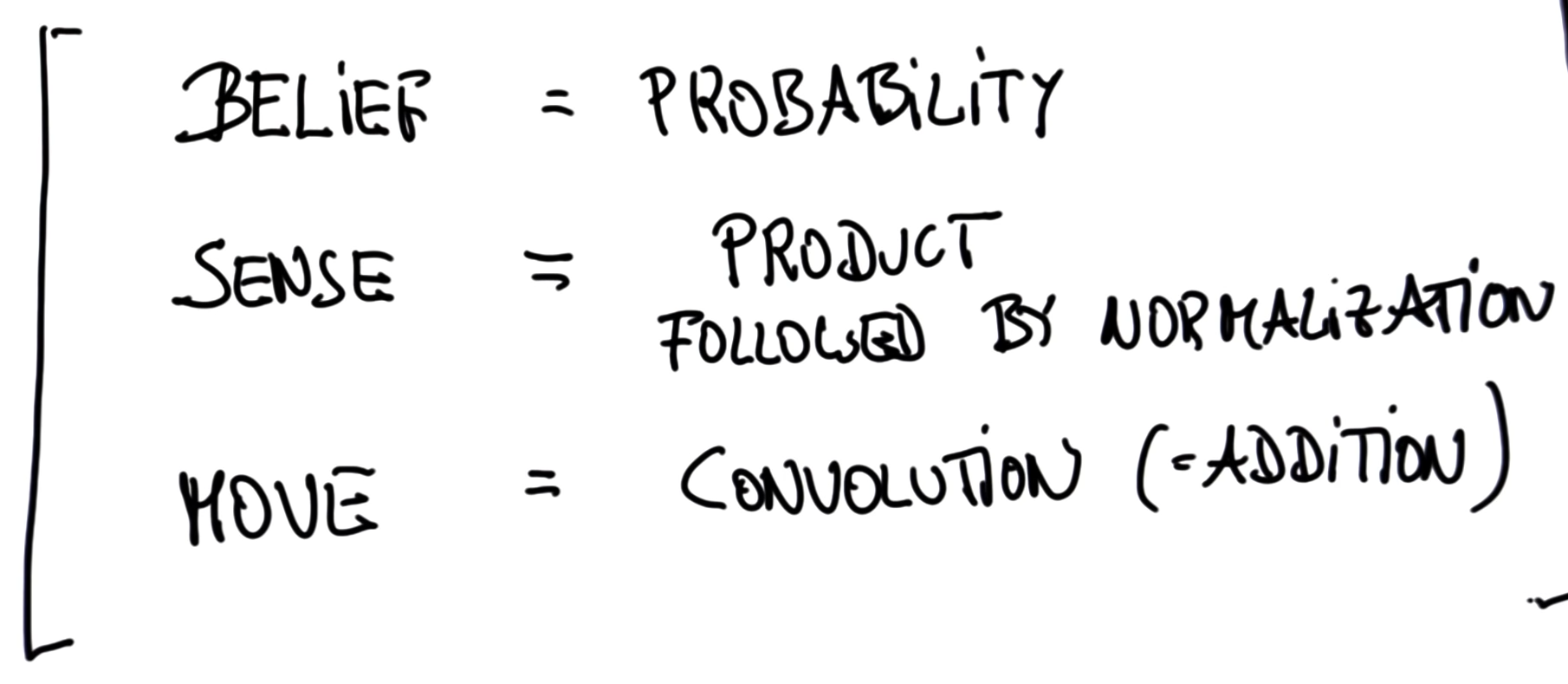
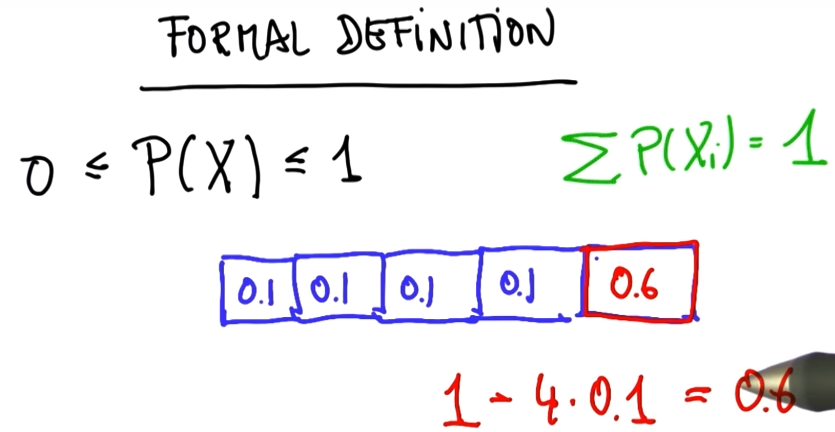
30. Formal Definition of Probability1

31. Formal Definition of Probability2

32. Formal Definition of Probability3
33. Bayes' Rule

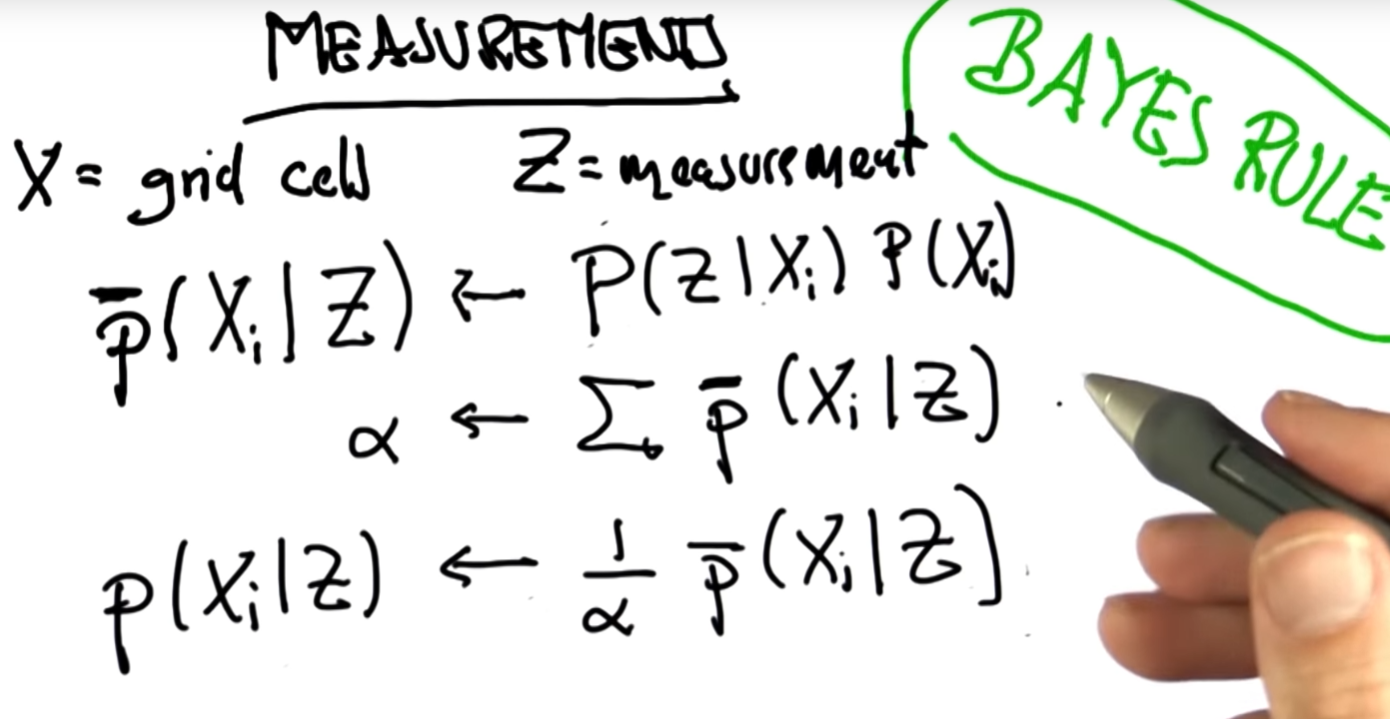
34. Cancer Test

35. Theorem of Total Probability
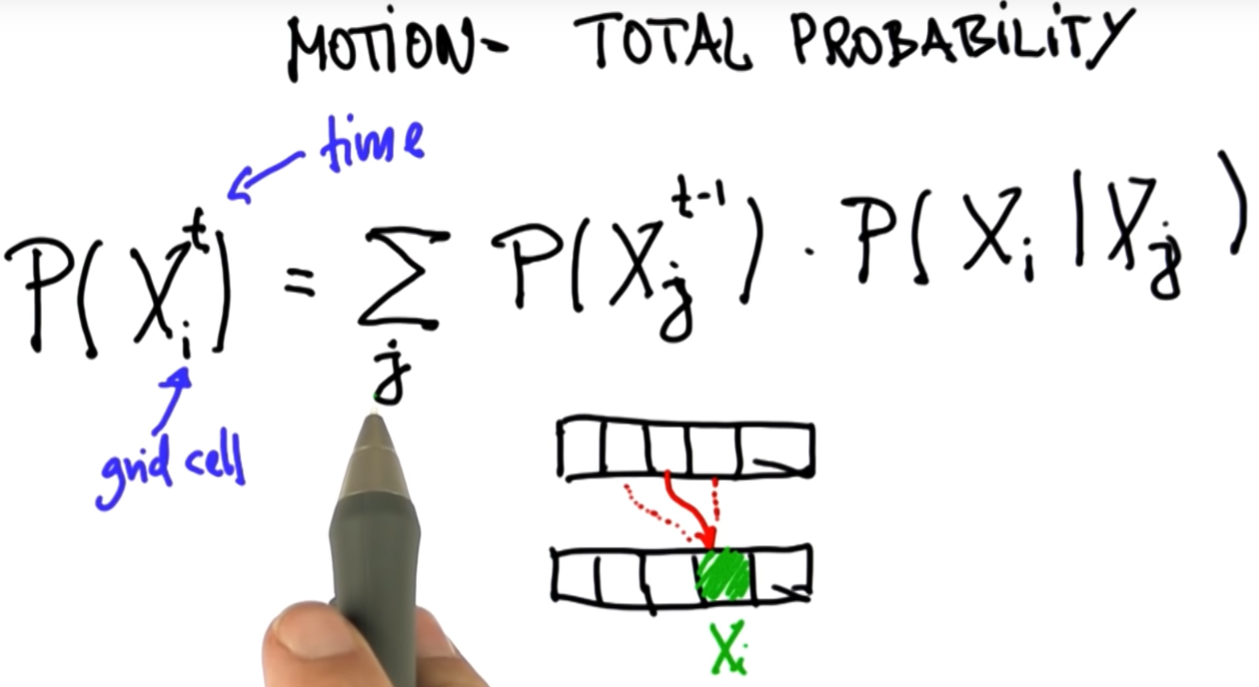

36. Coin Flip Quiz

37. Two Coin Quiz
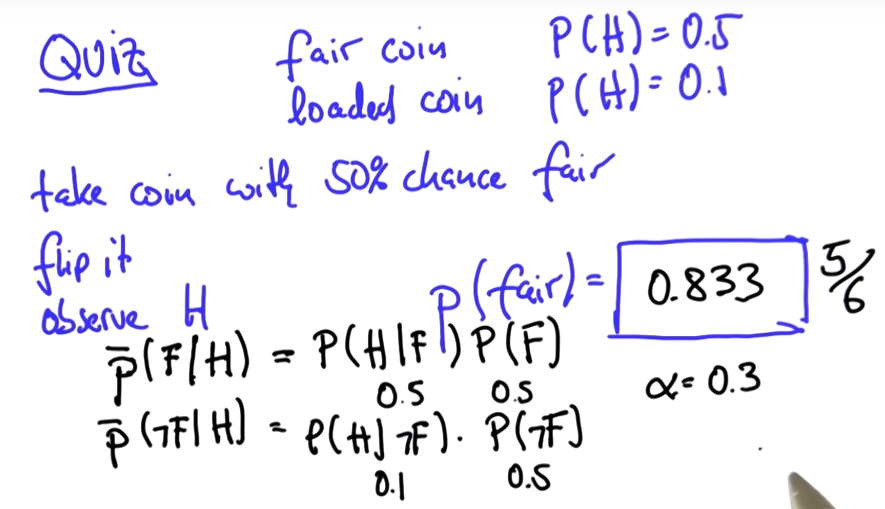
반응형