Virtual Force Field (VFF)

이 글은 아래의 논문을 토대로 구성되었습니다.

 

Borenstein, J., & Koren, Y. (1989). Real-time obstacle avoidance for fast mobile robots. 
IEEE Transactions on systems, Man, and Cybernetics, 19(5), 1179-1187.

 

VFF

---

가상의 froce field를 이용하여 로봇을 자율 주행

• repulsive force : occupied cell에 대하여 로봇이 척력과 같은 힘을 받음

 

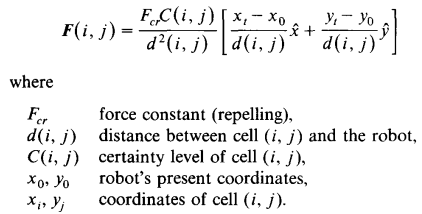
• resultant repulsive force : repulsive force에 대한 합력

 

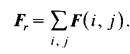
• attracting force : 목적지에 대하여 로봇이 인력과 같은 힘을 받음
  

  

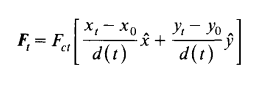
• resultant force : resultant repulsive force와 attracting force의 합력
  - 이 힘의 방향에 따라 장애물은 피하며 로봇이 목적지로 이동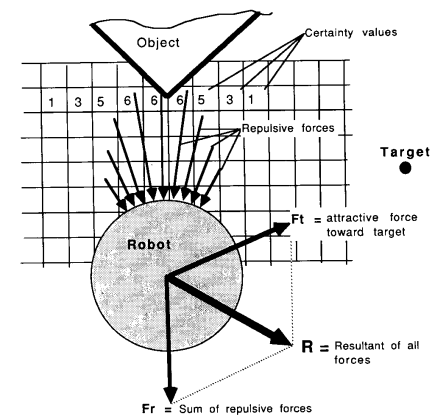
  

  

  

 

 

 

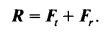
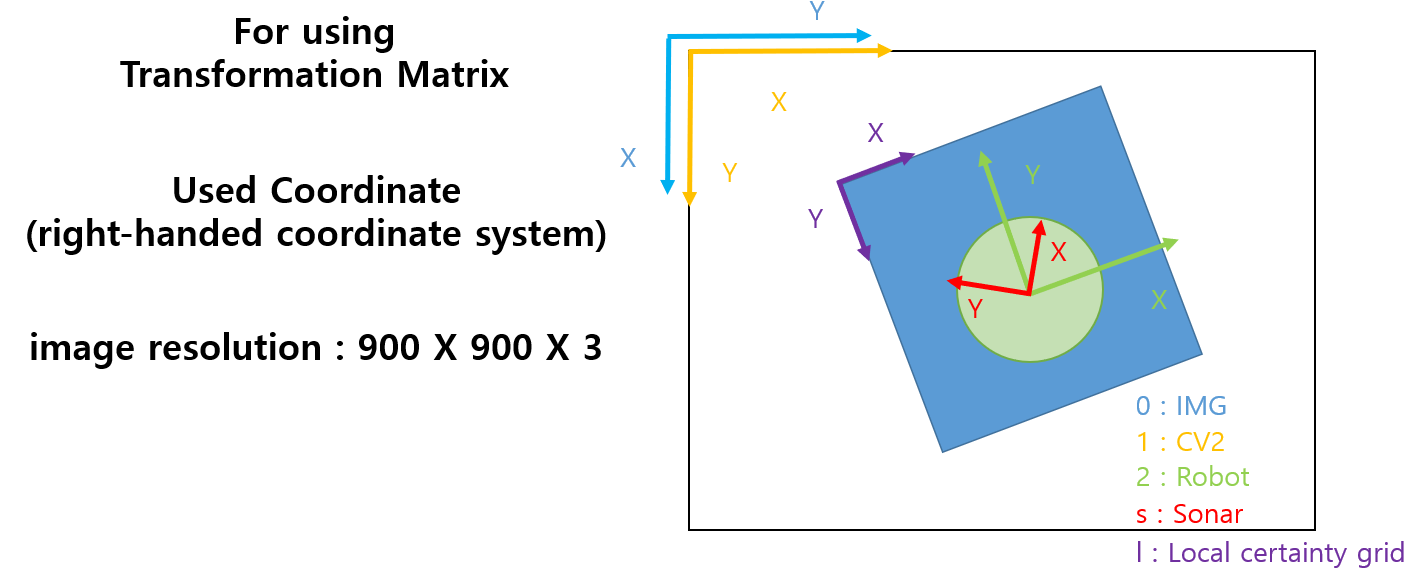
VFF를 활용한 Sonar-based mobile robot simulation (python 구현)

---

* TF를 위한 좌표계 설정

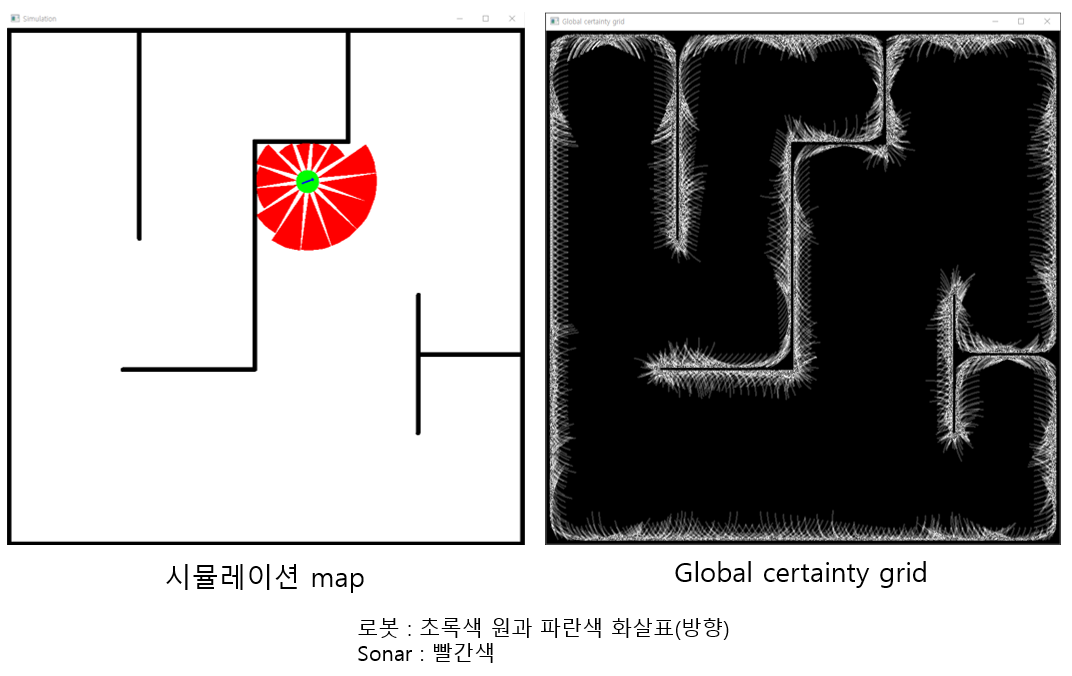
* 화면 구성

https://youtu.be/L1pymmTWv-c

 

 

 

프로그램했던 특징점

---

1) TF

원의 중심, 화살표의 시작, 목표지점에 대해 TF를 적용하여
많은 연산량을 줄이면서 위치를 쉽게 계산할 수 있었음

 

2) 개별 sonar에 대한 로봇과 장애물 거리 측정 함수 속도 개선

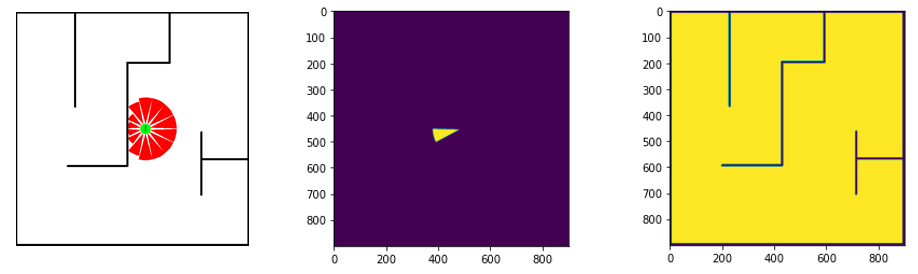
input : obs - 장애물에 대한 Global map

          position - Global map에 대한 sonar position

          sonar_area - 개별 sonar에 대한 Global map (R채널)

 

output : sonar의 검출된 장애물의 최소 거리

 

• 전체 이미지 사용 (단점 : Global map이 커질수록 속도가 느려짐)

 

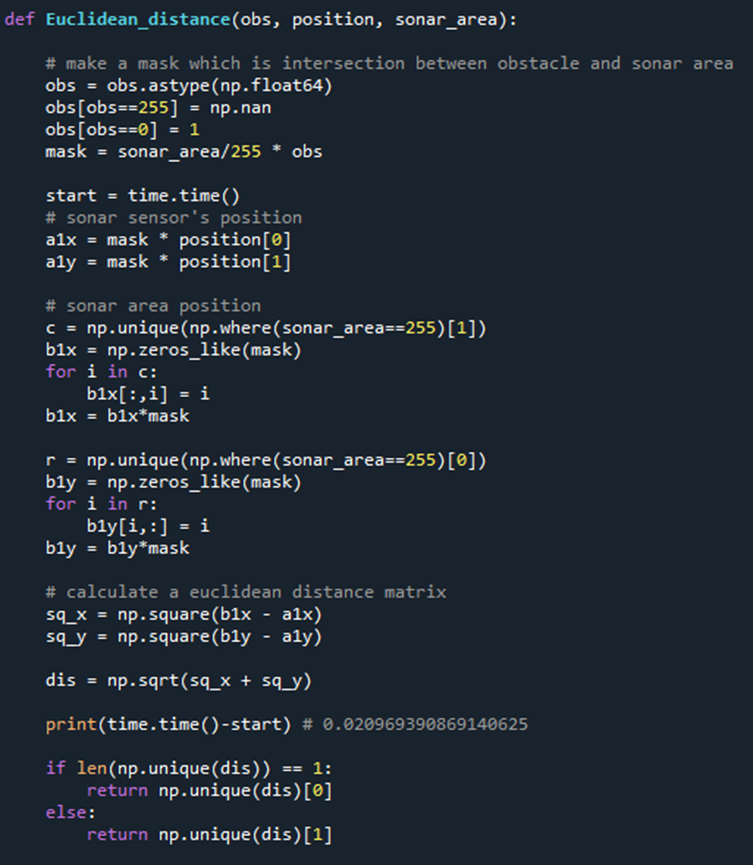
1개의 sonar에 대한 연산 시간 : 0.021sec

총 14개의 sonar에 대한 연산 시간 : 0.294sec

 

 

• mask의 인덱스를 이용한 연산

 

# 0 : img
# 1 : cv2
# 2 : robot
# s : sonar
# l : local certainty grid

# P_sonar : sonar sensor's position on cv2
# sonar_area : each sonar area on image which is channel 1

def Euclidean_distance(obs, P1_sonar, sonar_area):
    
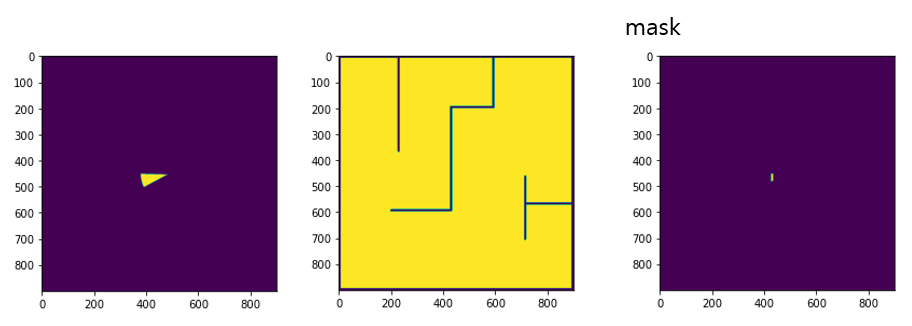
    # make a mask which is intersection between obstacle and sonar area
    obs = obs.astype(np.float64)
    obs[obs==255] = np.nan #empty
    obs[obs==0] = 1 # obstacle
    mask = sonar_area/255 * obs
    
    # start = time.time()
    
    idx = np.asarray(np.where(mask==1))
    # if don't detect a obstacle
    if idx.size==0:
        return np.nan
    Ps = np.array([[P1_sonar[1]], [P1_sonar[0]]]) # (y, x) in cv2 coordinate
    sq = np.square(Ps - idx)
    dis = np.sqrt(sq[0,:]+sq[1,:])
    m = int(np.min(dis))

    # print(time.time()-start) # 0.001990079879760742
    
    return m

 

1개의 sonar에 대한 연산 시간 : 0.002sec

총 14개의 sonar에 대한 연산 시간 : 0.028sec

 

따라서 속도를 10배 이상 개선