[Udacity] Lesson 4 : Kalman Filters

https://www.udacity.com/course/artificial-intelligence-for-robotics--cs373

Artificial Intelligence for Robotics | Free Courses | Udacity

https://github.com/jstar0525/ros_for_robotics/tree/main/artificial_intelligence_for_robotics/4_kalman_filter

GitHub - jstar0525/ros_for_robotics: ros for robotics

Lesson 4 : Kalman Filters

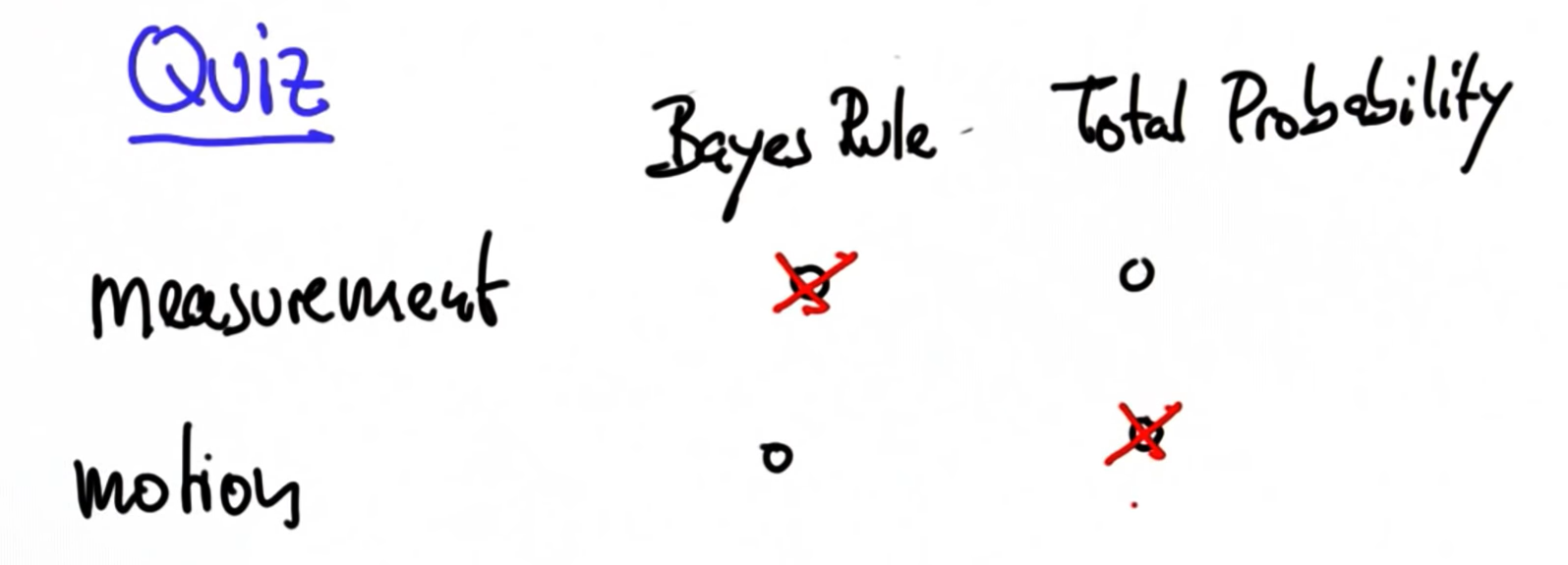
1. Introduction

2. Become a Professional

3. Tracking Intro

4. Gaussian Intro

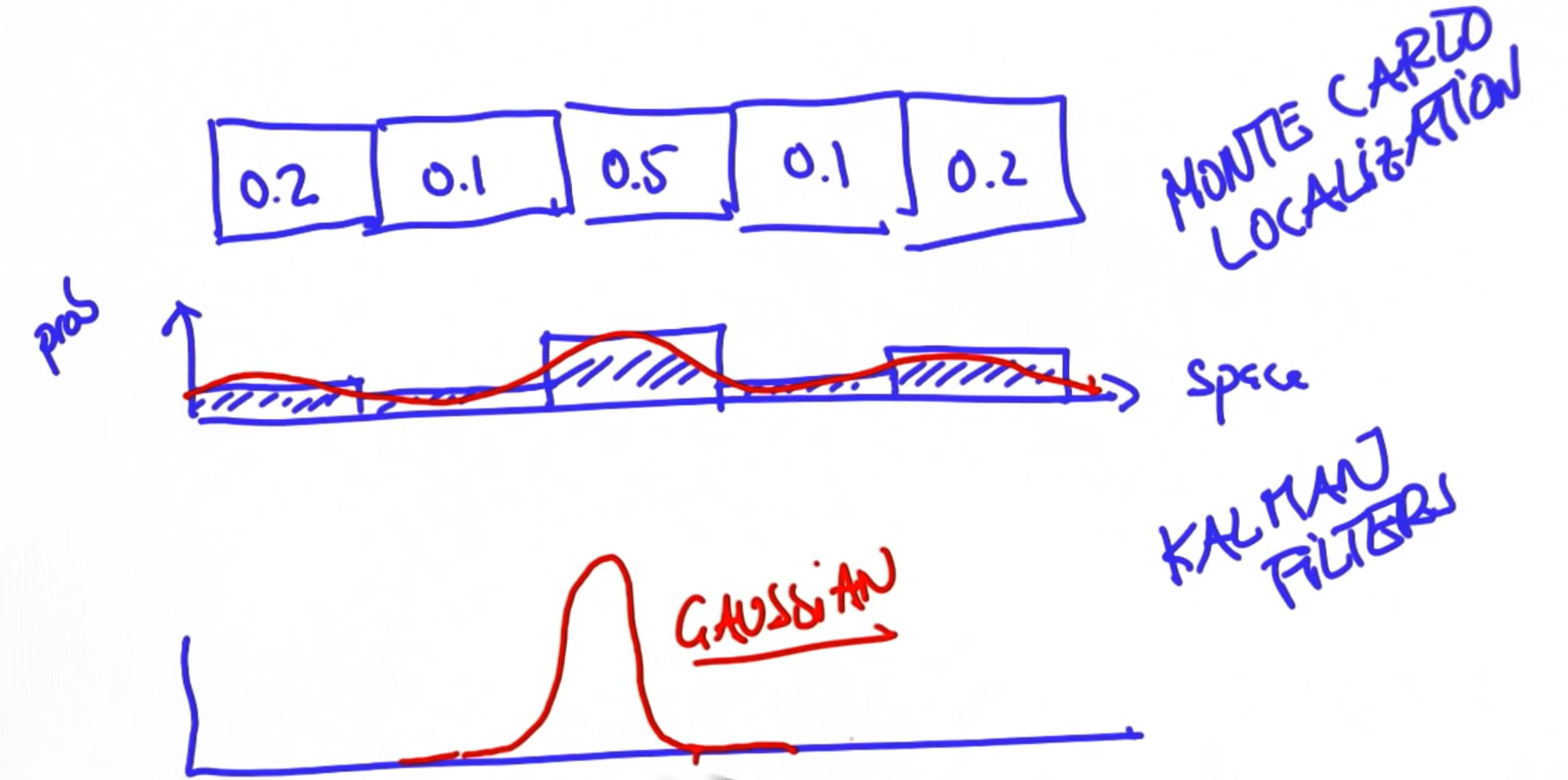
5. Variance Comparison

6. Preferred Gaussian

7. Evaluate Gaussian

8. Maximize Gaussian

#For this problem, you aren't writing any code.
#Instead, please just change the last argument 
#in f() to maximize the output.

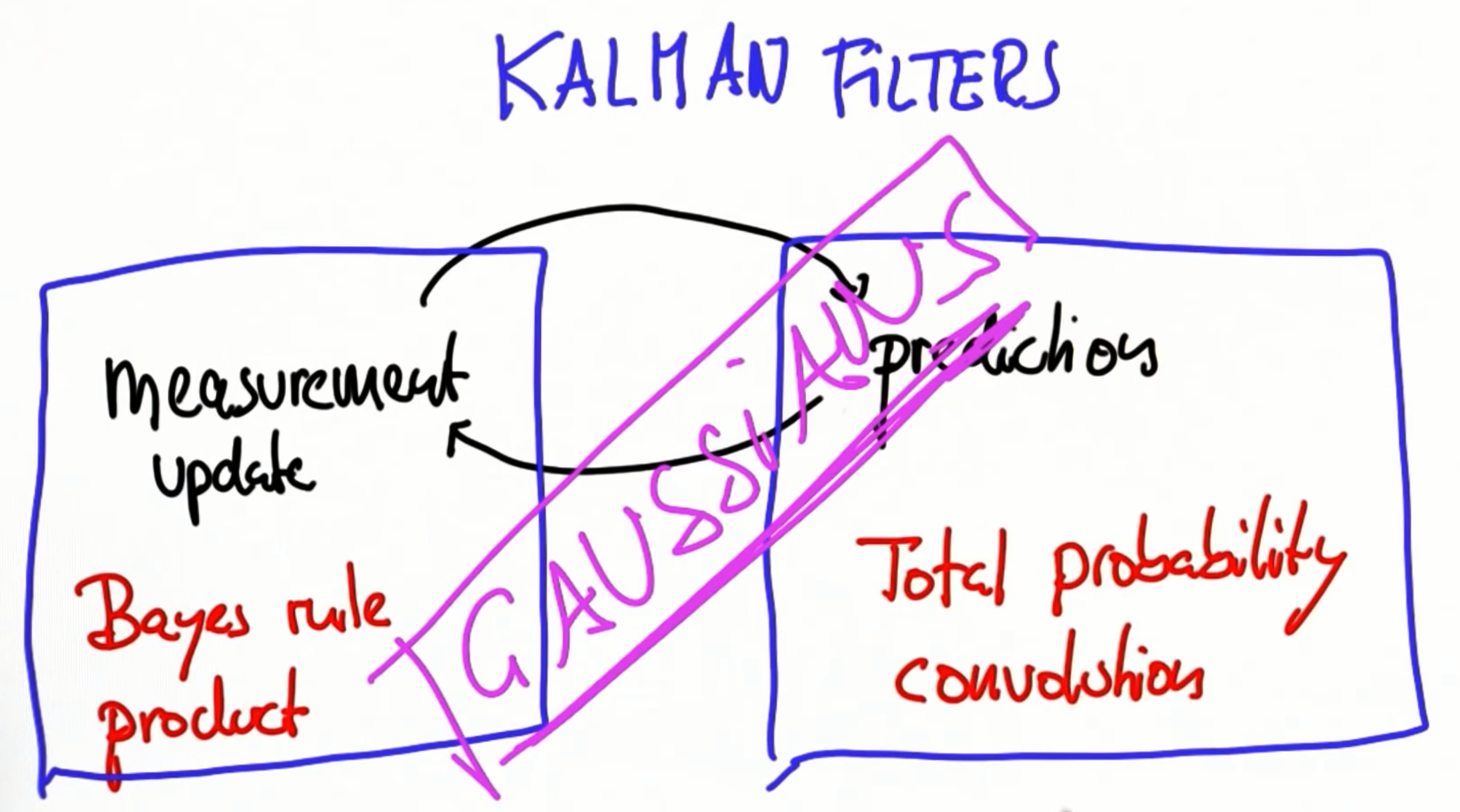
from math import *

def f(mu, sigma2, x):
    return 1/sqrt(2.*pi*sigma2) * exp(-.5*(x-mu)**2 / sigma2)

print(f(10.,4.,8.)) #Change the 8. to something else! # 0.12098536225957168
print(f(10.,4.,10.)) # 0.19947114020071635

9. Measurement and Motion1

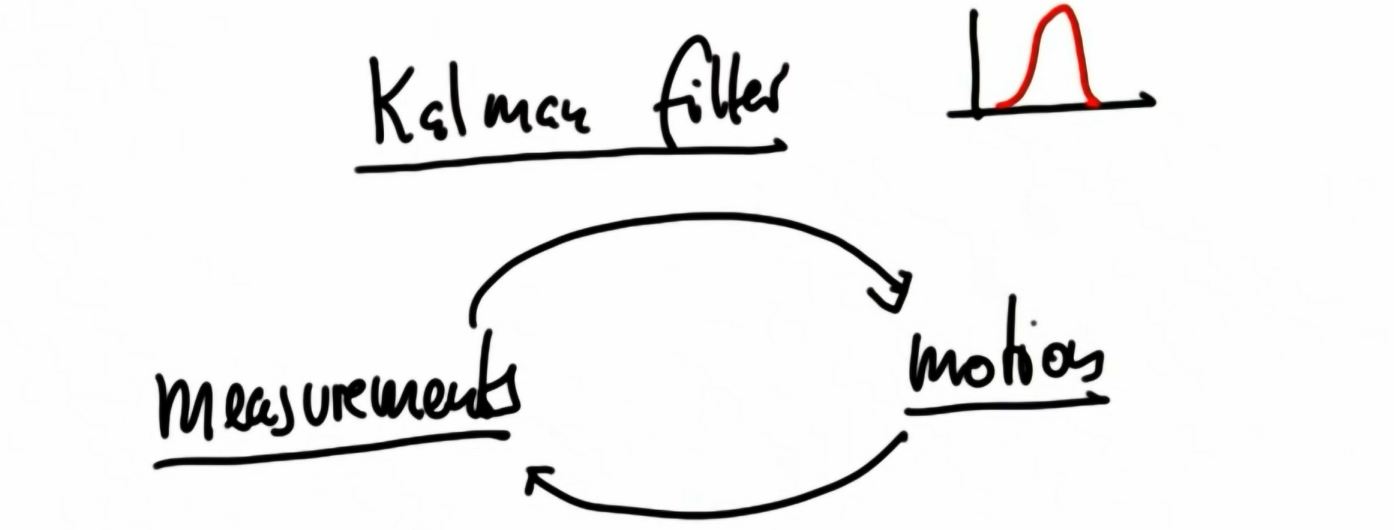
10. Shifting the Mean

10. Predicting the Peak

11. Parameter Update

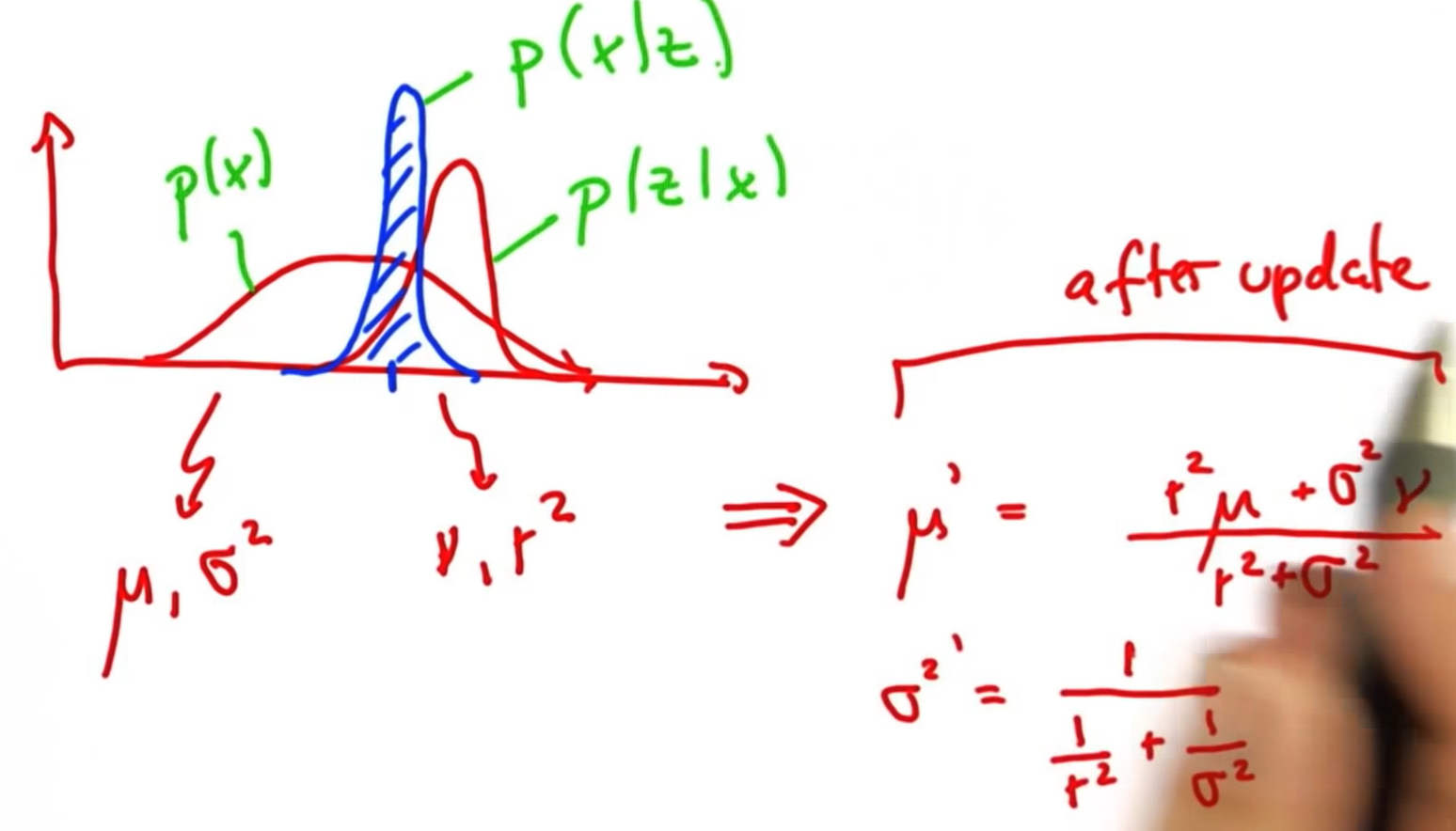
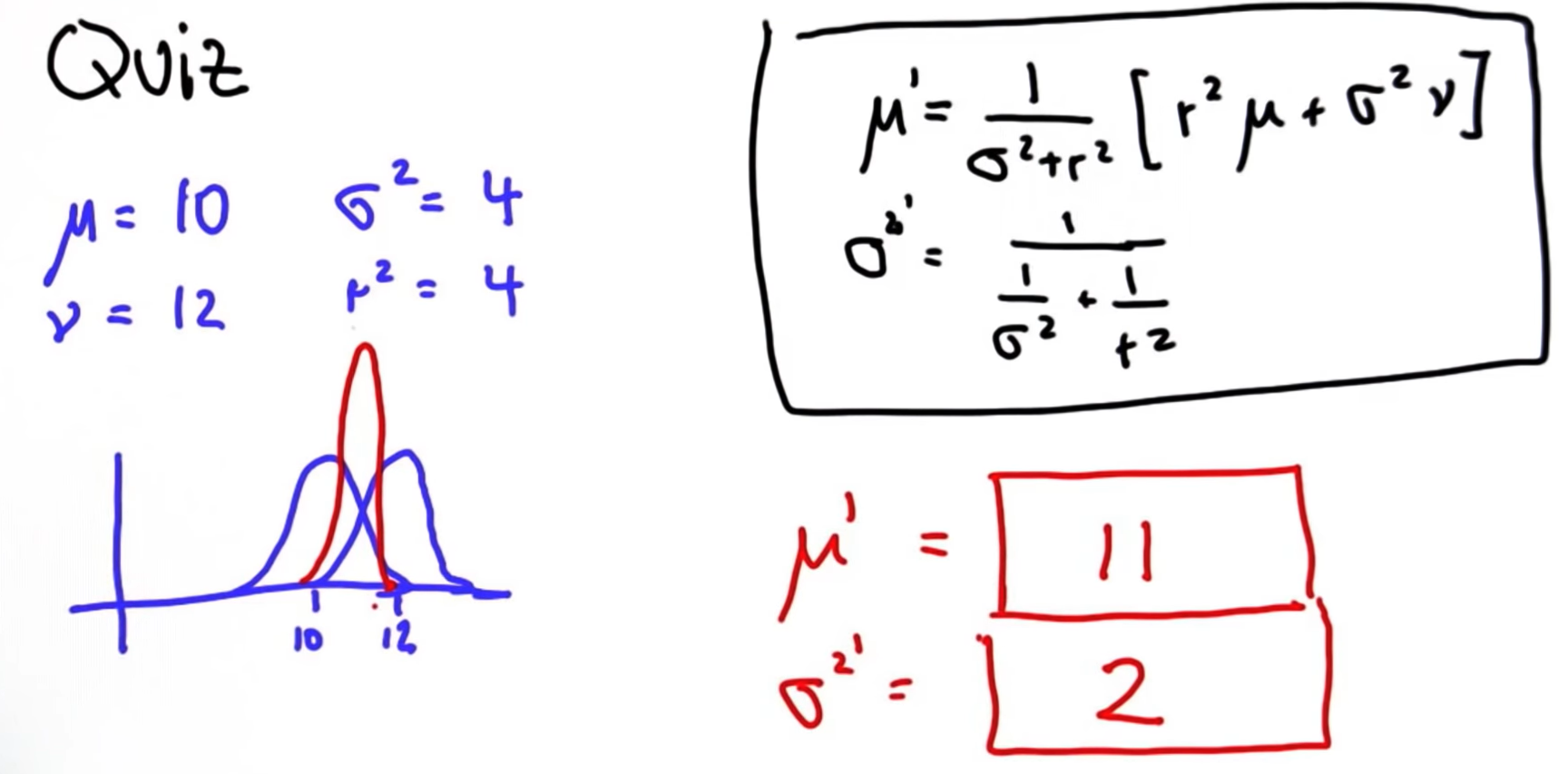
12. Parameter Update 2

13. Separated Gaussians

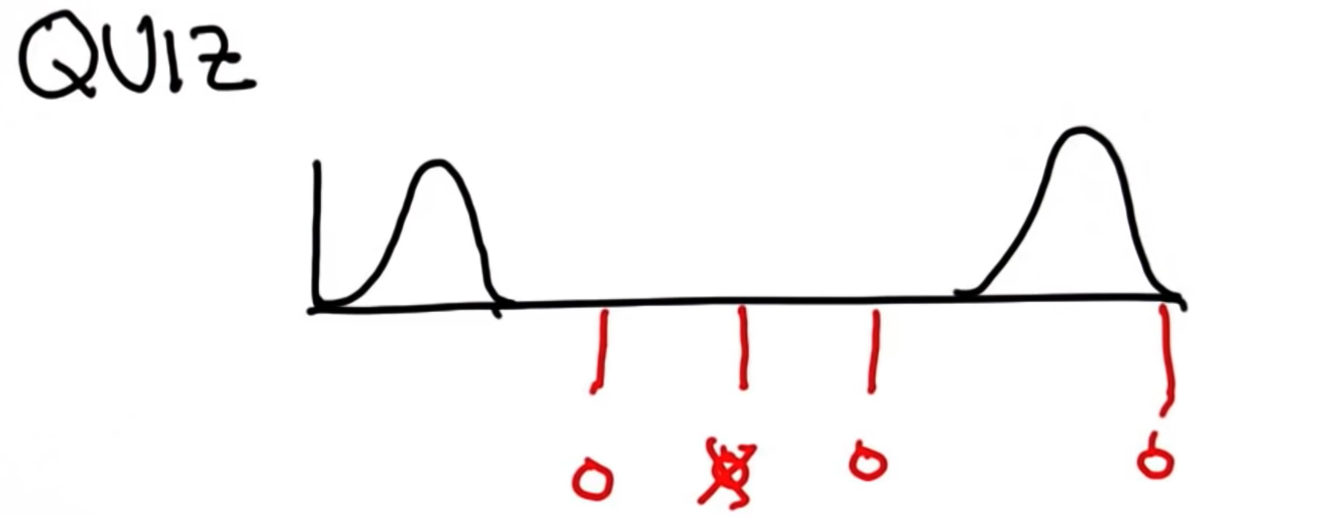
14. Separated Gaussians 2

15. New Mean and Variance

# Write a program to update your mean and variance
# when given the mean and variance of your belief
# and the mean and variance of your measurement.
# This program will update the parameters of your
# belief function.

def update(mean1, var1, mean2, var2):
    new_mean = (var1*mean2 + var2*mean1)/(var1 + var2)
    new_var = 1/(1/var1 + 1/var2)
    return [new_mean, new_var]

print update(10.,9.,13., 2.) # [12.454545454545455, 1.6363636363636362]

16. Gaussian Motion

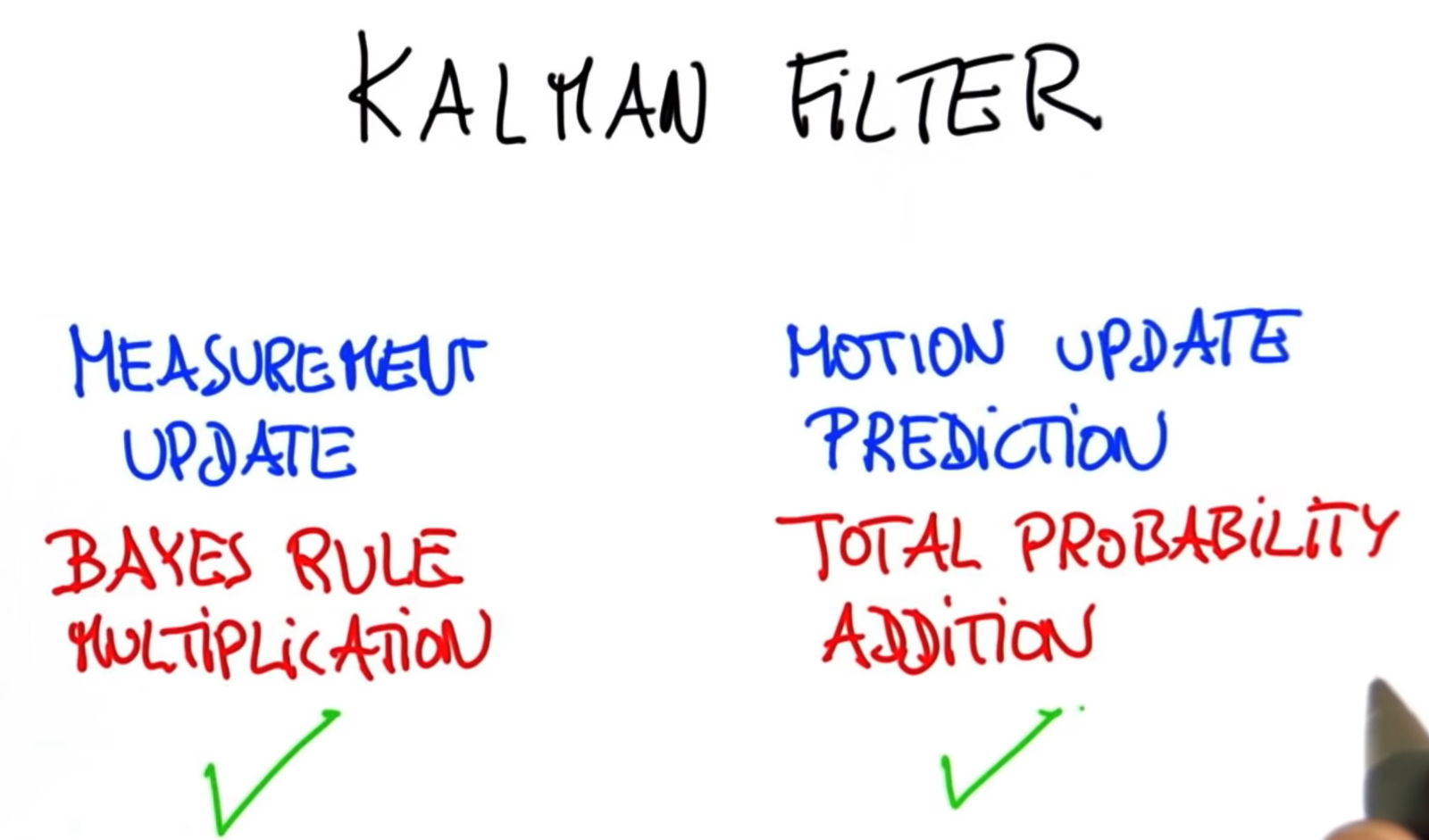
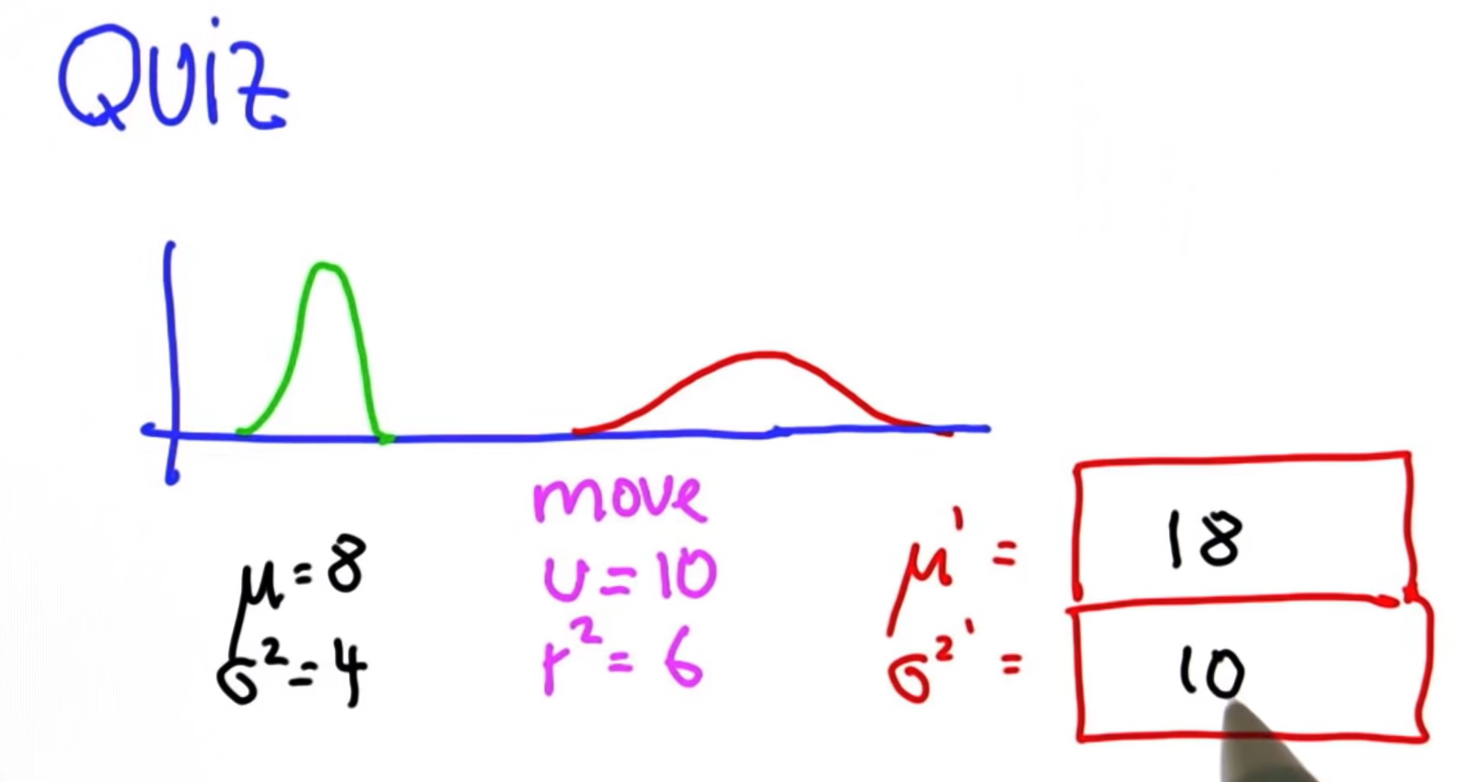
17. Predict Fuction

# Write a program that will predict your new mean
# and variance given the mean and variance of your 
# prior belief and the mean and variance of your 
# motion. 

def update(mean1, var1, mean2, var2):
    new_mean = (var2 * mean1 + var1 * mean2) / (var1 + var2)
    new_var = 1/(1/var1 + 1/var2)
    return [new_mean, new_var]

def predict(mean1, var1, mean2, var2):
    new_mean = mean1 + mean2
    new_var = var1 + var2
    return [new_mean, new_var]

print predict(10., 4., 12., 4.) # [22.0, 8.0]

18. Kalman Filter Code

# Write a program that will iteratively update and
# predict based on the location measurements 
# and inferred motions shown below. 

def update(mean1, var1, mean2, var2):
    new_mean = float(var2 * mean1 + var1 * mean2) / (var1 + var2)
    new_var = 1./(1./var1 + 1./var2)
    return [new_mean, new_var]

def predict(mean1, var1, mean2, var2):
    new_mean = mean1 + mean2
    new_var = var1 + var2
    return [new_mean, new_var]

measurements = [5., 6., 7., 9., 10.]
motion = [1., 1., 2., 1., 1.]
measurement_sig = 4.
motion_sig = 2.
mu = 0.
sig = 10000.

#Please print out ONLY the final values of the mean
#and the variance in a list [mu, sig]. 
for i in range(5):
    m = measurements[i]
    mm = motion[i]
    mu, sig = update(mu, sig, m, measurement_sig)
    mu, sig = predict(mu, sig, mm, motion_sig)
# Insert code here

print [mu, sig] # [10.999906177177365, 4.005861580844194]

19. Kalman Prediction

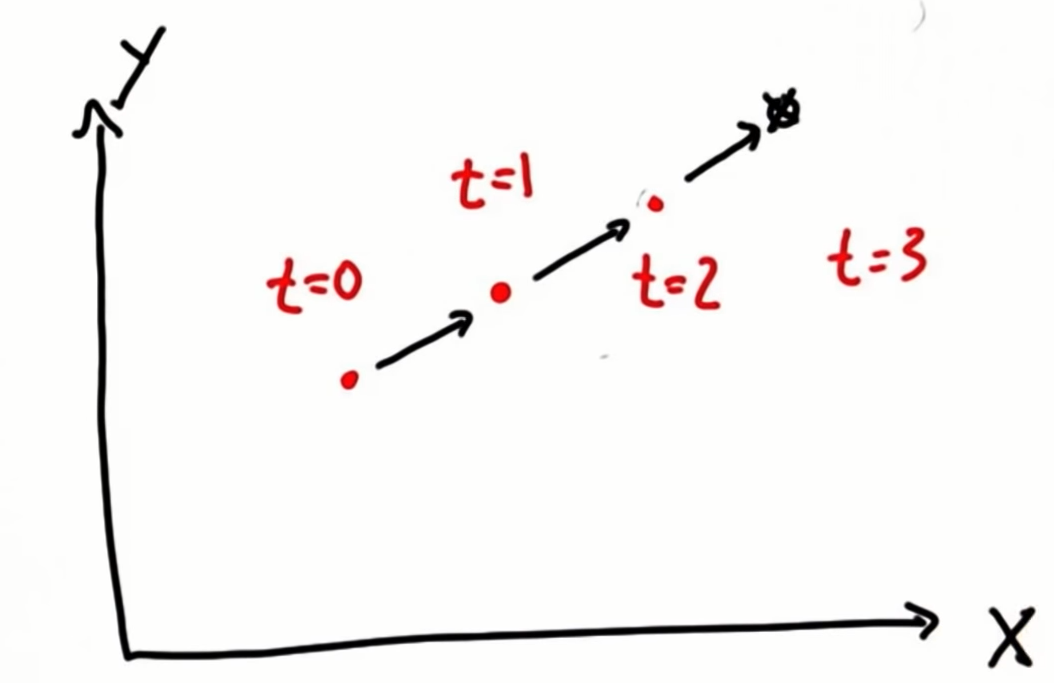
20. Kalman Filter Land

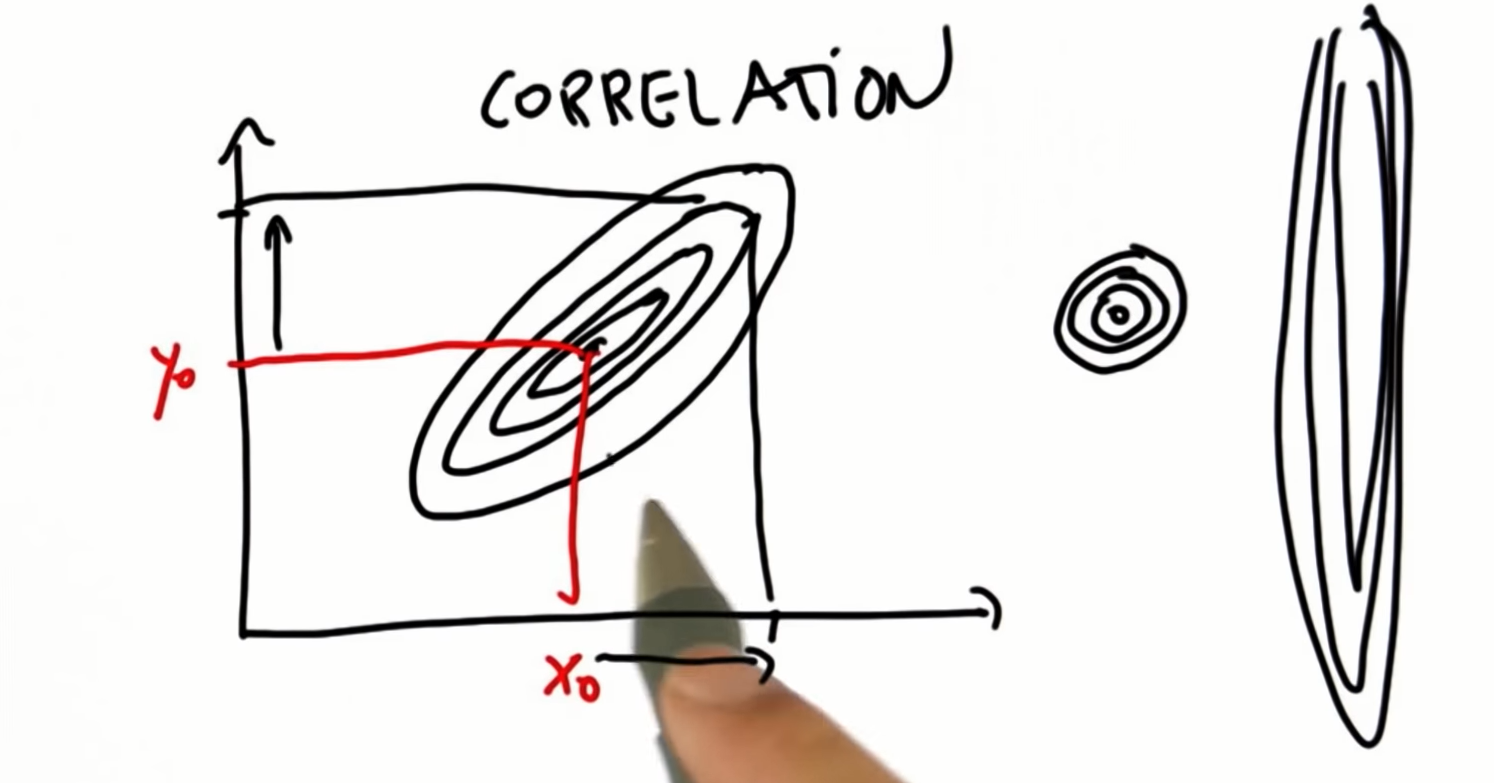
21. Kalman Filter Prediction

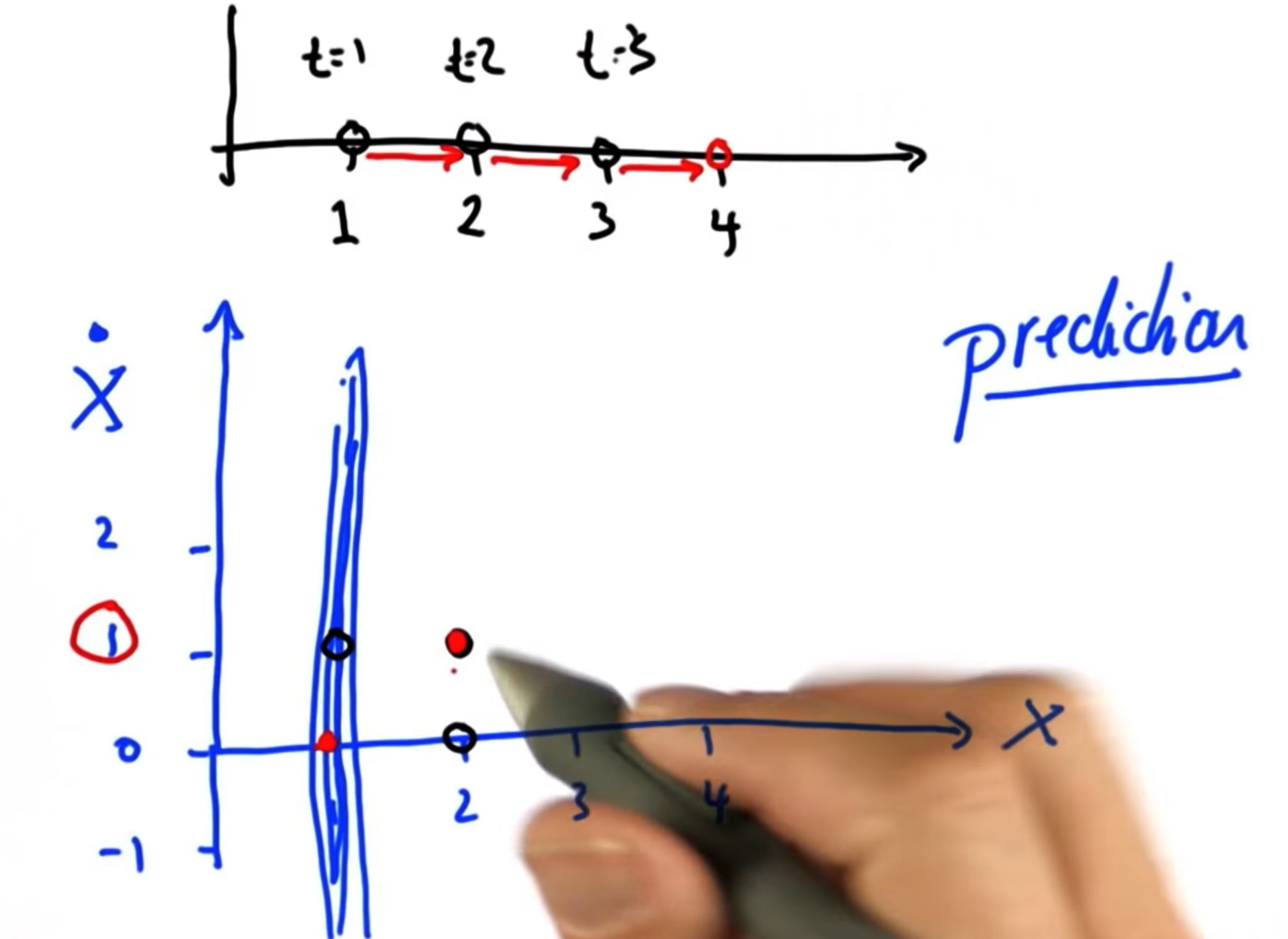
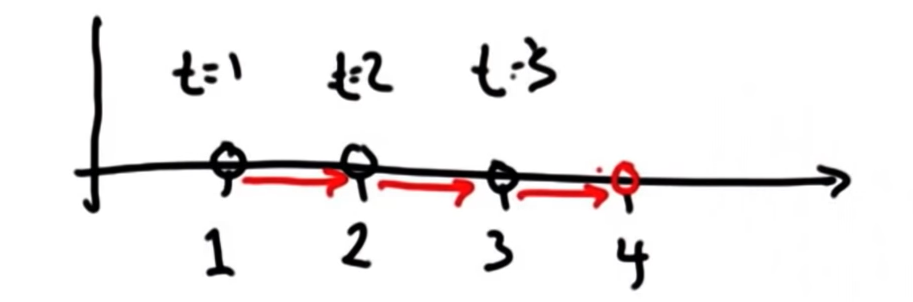
22. Another Prediction

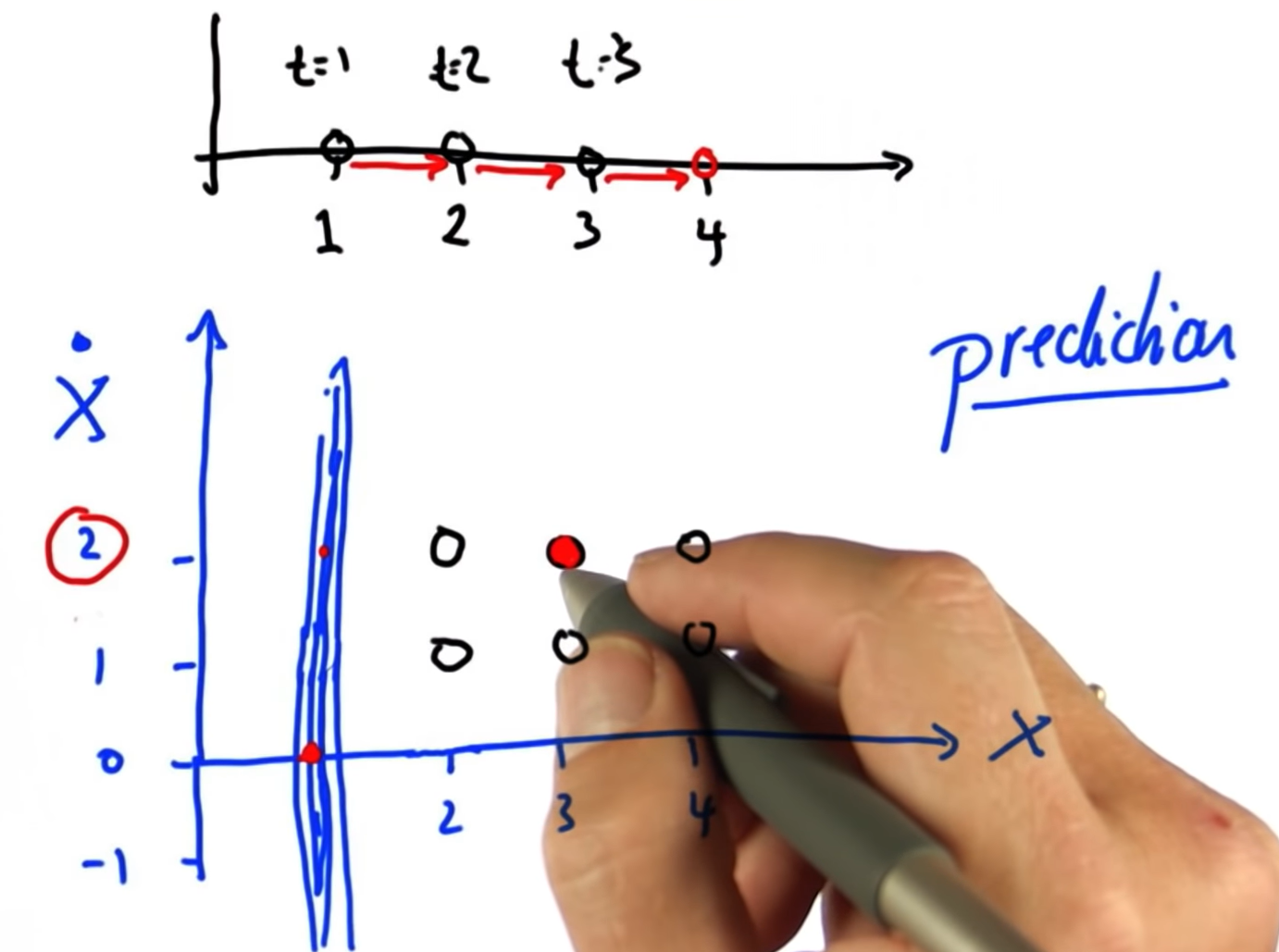
23. More Kalman Filters

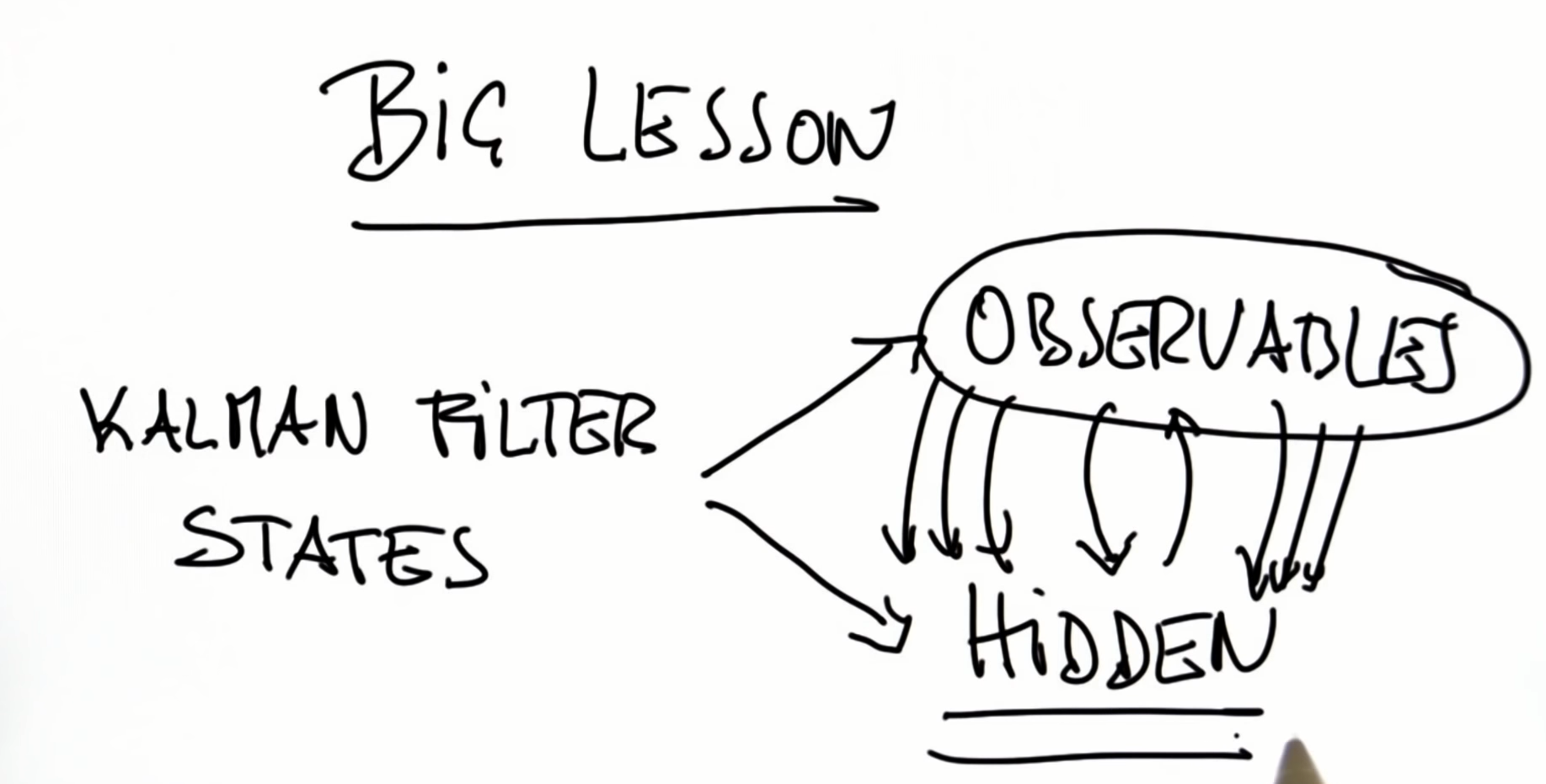
24. Kalman Filter Design

25. Kalman Matrices

# Write a function 'kalman_filter' that implements a multi-
# dimensional Kalman Filter for the example given

from math import *


class matrix:
    
    # implements basic operations of a matrix class
    
    def __init__(self, value):
        self.value = value
        self.dimx = len(value)
        self.dimy = len(value[0])
        if value == [[]]:
            self.dimx = 0
    
    def zero(self, dimx, dimy):
        # check if valid dimensions
        if dimx < 1 or dimy < 1:
            raise ValueError, "Invalid size of matrix"
        else:
            self.dimx = dimx
            self.dimy = dimy
            self.value = [[0 for row in range(dimy)] for col in range(dimx)]
    
    def identity(self, dim):
        # check if valid dimension
        if dim < 1:
            raise ValueError, "Invalid size of matrix"
        else:
            self.dimx = dim
            self.dimy = dim
            self.value = [[0 for row in range(dim)] for col in range(dim)]
            for i in range(dim):
                self.value[i][i] = 1
    
    def show(self):
        for i in range(self.dimx):
            print(self.value[i])
        print(' ')
    
    def __add__(self, other):
        # check if correct dimensions
        if self.dimx != other.dimx or self.dimy != other.dimy:
            raise ValueError, "Matrices must be of equal dimensions to add"
        else:
            # add if correct dimensions
            res = matrix([[]])
            res.zero(self.dimx, self.dimy)
            for i in range(self.dimx):
                for j in range(self.dimy):
                    res.value[i][j] = self.value[i][j] + other.value[i][j]
            return res
    
    def __sub__(self, other):
        # check if correct dimensions
        if self.dimx != other.dimx or self.dimy != other.dimy:
            raise ValueError, "Matrices must be of equal dimensions to subtract"
        else:
            # subtract if correct dimensions
            res = matrix([[]])
            res.zero(self.dimx, self.dimy)
            for i in range(self.dimx):
                for j in range(self.dimy):
                    res.value[i][j] = self.value[i][j] - other.value[i][j]
            return res
    
    def __mul__(self, other):
        # check if correct dimensions
        if self.dimy != other.dimx:
            raise ValueError, "Matrices must be m*n and n*p to multiply"
        else:
            # multiply if correct dimensions
            res = matrix([[]])
            res.zero(self.dimx, other.dimy)
            for i in range(self.dimx):
                for j in range(other.dimy):
                    for k in range(self.dimy):
                        res.value[i][j] += self.value[i][k] * other.value[k][j]
            return res
    
    def transpose(self):
        # compute transpose
        res = matrix([[]])
        res.zero(self.dimy, self.dimx)
        for i in range(self.dimx):
            for j in range(self.dimy):
                res.value[j][i] = self.value[i][j]
        return res
    
    # Thanks to Ernesto P. Adorio for use of Cholesky and CholeskyInverse functions
    
    def Cholesky(self, ztol=1.0e-5):
        # Computes the upper triangular Cholesky factorization of
        # a positive definite matrix.
        res = matrix([[]])
        res.zero(self.dimx, self.dimx)
        
        for i in range(self.dimx):
            S = sum([(res.value[k][i])**2 for k in range(i)])
            d = self.value[i][i] - S
            if abs(d) < ztol:
                res.value[i][i] = 0.0
            else:
                if d < 0.0:
                    raise ValueError, "Matrix not positive-definite"
                res.value[i][i] = sqrt(d)
            for j in range(i+1, self.dimx):
                S = sum([res.value[k][i] * res.value[k][j] for k in range(self.dimx)])
                if abs(S) < ztol:
                    S = 0.0
                try:
                   res.value[i][j] = (self.value[i][j] - S)/res.value[i][i]
                except:
                   raise ValueError, "Zero diagonal"
        return res
    
    def CholeskyInverse(self):
        # Computes inverse of matrix given its Cholesky upper Triangular
        # decomposition of matrix.
        res = matrix([[]])
        res.zero(self.dimx, self.dimx)
        
        # Backward step for inverse.
        for j in reversed(range(self.dimx)):
            tjj = self.value[j][j]
            S = sum([self.value[j][k]*res.value[j][k] for k in range(j+1, self.dimx)])
            res.value[j][j] = 1.0/tjj**2 - S/tjj
            for i in reversed(range(j)):
                res.value[j][i] = res.value[i][j] = -sum([self.value[i][k]*res.value[k][j] for k in range(i+1, self.dimx)])/self.value[i][i]
        return res
    
    def inverse(self):
        aux = self.Cholesky()
        res = aux.CholeskyInverse()
        return res
    
    def __repr__(self):
        return repr(self.value)


########################################

# Implement the filter function below

def kalman_filter(x, P):
    for n in range(len(measurements)):
        z = matrix([[measurements[n]]])
        # print(z)
        # measurement update
        y = z.__sub__(H.__mul__(x))
        # print(y)
        S = H.__mul__(P).__mul__(H.transpose()).__add__(R)
        # print(S)
        K = P.__mul__(H.transpose()).__mul__(S.inverse())
        # print(K)
        x = x.__add__(K.__mul__(y))
        # print(x)
        P = (I.__sub__(K.__mul__(H))).__mul__(P)
        # print(I)
        # prediction
        x = F.__mul__(x).__add__(u)
        # print(x)
        P = F.__mul__(P).__mul__(F.transpose())
        # print(P)
        
    return x,P

############################################
### use the code below to test your filter!
############################################

measurements = [1, 2, 3]

x = matrix([[0.], [0.]]) # initial state (location and velocity)
P = matrix([[1000., 0.], [0., 1000.]]) # initial uncertainty
u = matrix([[0.], [0.]]) # external motion
F = matrix([[1., 1.], [0, 1.]]) # next state function
H = matrix([[1., 0.]]) # measurement function
R = matrix([[1.]]) # measurement uncertainty
I = matrix([[1., 0.], [0., 1.]]) # identity matrix

print(kalman_filter(x, P))
# output should be:
# x: [[3.9996664447958645], [0.9999998335552873]]
# P: [[2.3318904241194827, 0.9991676099921091], [0.9991676099921067, 0.49950058263974184]]

26. Conclusion